RIDDLER CLASSIC PUZZLE 11-26-2021
Trig the turkey cannot fly. And so, instead of flying, he decides to jump as far as he can with a running start up one of the famed Sinusoidal Hills, all of which are precisely the same size.
Trig knows that he cannot jump a horizontal distance of more than two hills. Also, he prefers a smooth takeoff and landing. That is, when he takes off from the ground and lands on it again, the slope of his parabolic trajectory through the air must perfectly match the instantaneous slope of the ground beneath him.
The animation below shows a jump where the takeoff and landing are precisely 1.2 hills apart.
What is the greatest horizontal distance Trig can jump, such that his takeoff and landing are smooth? Again, keep in mind that Trig cannot possibly jump a horizontal distance greater than two hills.
SOLUTION

SOLUTION
Because Trig can't jump a distance greater than two hills, he can only clear two peaks at best (since clearing 3 peaks would mean traveling a distance greater than two hills).
So we expect Trig to travel a maximum distance close to the 1.2 hills he did in the problem statement.
But can he do better ?
Let's see...
First, we simplify the problem by inverting the animation and asking an equivalent question:
Given an upward facing parabola (symmetrical about the y-axis) that 'contains' the cosine function in the interval [-2π, 2π],
how far apart can two of its points be tangent to the cosine function ?

Let:
f(x) = ax^2 + b be the parabola (where a > 0)
and
g(x) = cos(x) be the cosine function
* We'll measure in radians and restrict our domain to [0, 2π] to find the right-most point, and use symmetry to get the left-most point.
If g(x) - f(x) is the vertical distance from the parabola to the cosine function, then the conditions of the problem require that g(x) - f(x) attain a local minimum (or inflection point).
In other words, for some point p:
g'(p) - f'(p) = 0 and g''(p) - f''(p) ≥ 0
Thus,
-2ap = sin(p) and -2a ≥ cos(p)
So sin(p) and cos(p) are negative, and we just need to consider the third quadrant [π, 3π/2] after combining both equations:
p ≥ tan(p)
And the largest value p in the interval which this is true is approximately 4.4934 radians.
By symmetry, the other point is approximately -4.4934 radians.
So the maximum total distance Trig can travel is about 8.9868 radians, or
8.9868 / 2π ≈ 1.43 hills
Additional notes: Given p ≈ 4.4934 radians, we can also solve for an approximate equation of the parabola and plot it along with the cosine function:
f(x) ≈ .1086 x^2 - 2.41
g(x) = cos(x)
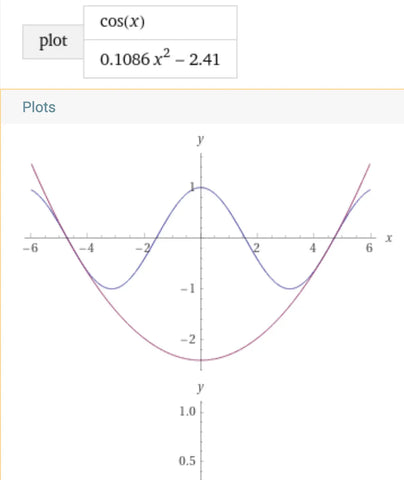
To recover the original sinusoidal landscape and Trig's flight trajectory, we just invert the plots and add 1:
Sinusoidal Hills = 1 - cos(x)
Trig's flight trajectory ≈ 3.41 - .1086 x^2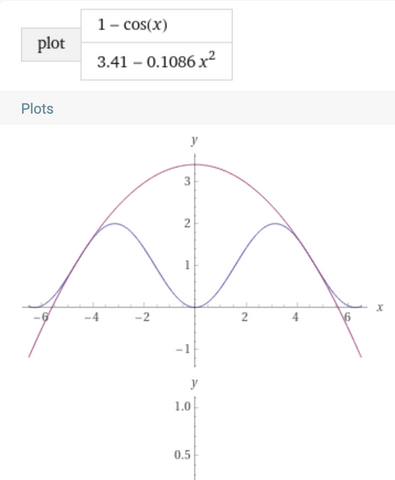





















Hi,
Thanks for the write up. I had a similar (but not the same) approach which you can read here: https://www.starvind.com/math/projectile-turkey/
We eventually end up with the same criteria but through different reasoning. I use the second derivative to ensure that Trig’s trajectory stays over the hill at all times vs. slamming into it.
Leave a comment