RIDDLER CLASSIC PUZZLE 1-07-2022
Amare the ant is traveling within Triangle ABC, as shown below. Angle A measures 15 degrees, and sides AB and AC both have length 1.
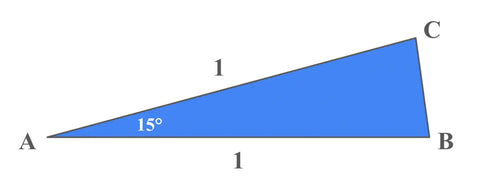
Amare starts at point B and wants to ultimately arrive on side AC. However, the queen of his colony has asked him to make several stops along the way. Specifically, his path must:
- Start at point B.
- Second, touch a point — any point — on side AC.
- Third, touch a point — any point — back on side AB.
- Finally, proceed to a point — any point — on side AC (not necessarily the same point he touched earlier).
What is the shortest distance Amare can travel to complete the queen’s desired path?
SOLUTION
Supplement the above triangle ABC with its mirror reflections and consider an arbitrary path traveled by Amare:
B --> 1 --> 2 --> 3
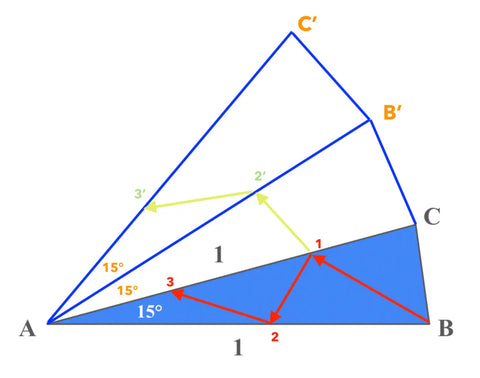
Amare's path can also be viewed as it's mirror equivalent: B --> 1 --> 2' --> 3'
Since both paths have the same length, the shortest path for Amare will be the shortest path from B --> 3', which is just a straight line perpendicular to AC'.
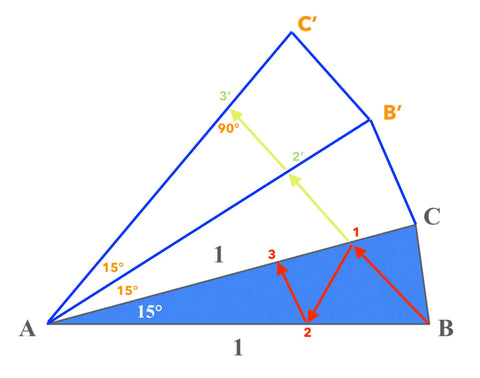
Since this forms one of the legs of a 45° 45° 90° triangle with hypotenuse 1, the distance B --> 3' is just:
1/√2





















Leave a comment